3种移位:
逻辑右移 >>
逻辑左移 <<
算术右移 >> (针对有符号数,高位补符号)
计算机中的除法是整除 ,整除带来的问题就是取整
对于正数来说: 向下取整
对于负数来说: 向上取整
因此计算机除法是 向0取整
0011 2 >> 1 0001 => 1 向下取整
1101 -3 >> 1 1110 => -2 向下取整
从上面可以看出,右移是向下取整的
除法的优化
除法优化的前提是除数是常量
伪造出来的M 计算结果可能精度不够, 计算 除数是 精度 应该是小数点后 6个9再取整
计算除数:
根据 M值 来判断
\1. 正数 y = 2^n / M
\2. 负数 y = 2^n / (2^32 - M)
\3. 溢出 y = 2^n / (2^32 + M)
1. 除数为无符号2的幂/
在cpu中,移位的效率高于算术运算
对于无符号数来说因此右移可以取代除法,因为 2者的 取整方式一样,
x / 2^n = x >> n
2. 除数为有符号2的幂
当除数为正数时,跟上面的一致,当x位负数时,取整方向发生了改变,因此需要把向下取整转为向上取整
下整转上整方式:
- 结果 + 1
- 被除数 + 一个数 2^n - 1 (调大被除数,结果也会变大),
例如: -10 / 4 向上取整 = (-10 + 3) / 4 向下取整
x >= 0
x / 2^n = (x + 0) >> n
x < 0
x / 2^n = (x + 2^n-1) >> n
分支慢的原因是因为会断流水线
指令实现无分支 正数 + 0 ,负数 + 15
cdq 这条指令 只有 intel 的cpu才有,因此跨平台的不能用这条指令
方法1:
mov eax, esi
cdq
and edx, 0Fh
add eax, edx
sar eax, 4
方法2:
mov edx, eax
sar edx, 31
and edx, 15
add eax, edx
sar eax, 4
方法3:
mov edx, eax
sar edx, 31 //正数全0 ,负数全1
shr edx, 28 // 高位补0
add eax, edx
sar eax, 4
3. 除数为有符号-2的幂
x / - 2^n = - ( x / 2^n )
4. 无符号非2的幂1
编译器是先乘一个数,再来位移 ,这个数编译器会先算出来 Magic Numbe
x / y = ( x * M ) >> n
=>
y = 2^n / M
对于32位系统来说 n 是一个 大于 32 的值 ,64位系统来说就是 大于64的值
5. 有符号非2的幂1 M >= 0
当 x 小于0 需要把向下取整转成向上取整, 而 向上取整 = 向下取整 + 1
所以 此公式 就变成了 x >= 0 结果 +0 和 x< 0 结果 + 1 的问题
x >= 0
x / y = (x * M) >> n + 0
x < 0
x / y = ((x * M) >> n) + 1
=>
y = 2^n / M
这个公式是最常见的 ,基本占 70% ~ 80%
无分支实现 正数 +0 负数 +1
mov eax , edx
shr eax , 1Fh ;取符号位
add eax , edx
6. 有符号负非2的幂1 M < 0
此式跟上式的区别就是 Magic Numbe 的最高位是 1
x / -y = ( x * -M ) >> n + 0
=>
y = 2^n / (2^32 - M)
7. 有符号非2的幂2 M < 0
取 Magic Numbe 值较大,本来是正数 ,但是因为是有符号,在 乘 的时候被当成了负数 ,此时计算结果会变小(变成了负数), 因此需要加上 变小的差值
x >= 0
x / y = (((x * M) >> 32) + x >> n) + 0
x < 0
x / y = (((x * M) >> 32) + x >> n) + 1
=>
y = 2^n / M
8. 有符号负非2的幂2 M >= 0
求负数的时候,就会造成 M >=0 (对M求完补码溢出变正数) ,此时计算结果会变大, 因此需要减去 变大的差值
x >= 0
x / y = (((x * M) >> 32) - x >> n) + 0
x < 0
x / y = (((x * M) >> 32) - x >> n) + 1
=>
y = 2^n / (2^32 - M)
9. 无符号非2的幂2
因为是无符号 Magic Numbe 可能会是一个很大很大的数, 乘完之后结果放不下,因此需要 分2次乘 2此移
公式: mul sub shr add shr
x / y = (x - (x * M) >> 32) >> n1) + (x * M >> 32) >> n2
=》
y = 2^n / (2^32 + M)
总结
当我们碰到一个除法,首先判断 除数是不是 2的 幂 ,不满足就看第二个公式(4.,5,6),还不满足就看 + (7) - (9) ,还不满足就看是否满足 乘 减 移 加 移 (9)
int n1 = 0;
int n2 = 0;
int n3 = 0;
scanf_s("%d %d", &n1, &n2);
n3 = (n1 / 7) * (n2 / 8) + (n2 / 5);
printf("%d\n", n3);
反汇编代码:
lea eax, [ebp+var_8]
mov dword ptr [ebp+Arglist], 0
push eax
lea eax, [ebp+Arglist]
mov [ebp+var_8], 0
push eax ; Arglist
push offset aDD ; "%d %d"
call sub_401050
mov eax, [ebp+var_8]
cdq
and edx, 7
lea edi, [edx+eax]
mov eax, 92492493h
imul dword ptr [ebp+Arglist]
mov eax, 66666667h
sar edi, 3 ; edi = n2 / 8
add edx, dword ptr [ebp+Arglist]
sar edx, 2
mov ecx, edx
shr ecx, 1Fh
add ecx, edx ; ecx = n1/7
imul [ebp+var_8]
imul edi, ecx ; edi = (n2 / 8) * (n1/7)
mov eax, edx
shr eax, 1Fh
add edi, edx ; edi = (n2 / 8) (n1/7) + ( n2 M >> n )
add eax, edi ; eax = (n2 / 8) (n1/7) + ( n2 M >> n ) +1
push eax
push offset Format ; "%d\n"
call sub_401020
=> edi = (n2 / 8) (n1 / 7) +( n2 M >> 32 ) +1
=> (n2 / 8) * (n1 / 7) + ( ( n2 * M >> n ) +1 )
=> (n2 / 8) * ( n1 / 7 ) + ( n2 / 5 )
取模
一个数 % 该数进制的 n 次幂 = 取 该数的 低 n-1 位
1.有符号模2的幂1 (新公式)
x >= 0
x % 2^n = x & 2^n - 1
x < 0 ;把负数变正数 (先加一个数再减去该数)
x % 2^n = x + ( 2^n - 1 & 2^n - 1 ) - 2^n - 1
例如: -6 % 8 = - 6 + 7 & 7 - 7
无分支实现
mov eax, ecx
cdq
and edx, 2^n-1
add ecx, edx
and ecx, 2^n-1
sub ecx edx
2.模2的幂2 (旧公式)
jns 分支跳转
if (x > 0)
x & 2^n - 1
else
(x - 1) | ~(2^n - 1) + 1
上式无法实现无分支是因为 没有规律
3.模非2的幂
x % y = z
=》
z = x - ( x / y ) * y
识别操作数符号
跳转指令 Jxx A B (无符号) (L G) 有符号
乘法 除法 有符号(i) 无符号(无)
加法减法不区分符号 (补码 把减法转成了 加法)
补码能取代减法 是因为 膜
膜最早出现再手表中: 代表可表示数的极限值 例如手表是 12
例如 要表示 3点 - 2点 = 1点 =》 3点 + ( 12点 - 2点 ) = 1点
即 一个数 - 另一个数 = 一个数 + ( 膜 - 另一个数 )
补码是为了迅速求出 膜 - 另一个数
IDA的使用
颜色条

表示整个软件的代码的分析结果
粉色: 表示导入表(这个节的代码不需要还原)
蓝色: 用户写的代码 (需要还原的代码),IDA可能会把库函数识别成自己的代码
浅蓝色:库函数(静态链接进来的)(不需要还原)
灰色: 数据
浅黄色:数据 :全局数据区
图视图
方便快速看分支
一个方格代表一个代码块
当代码量很大的时候,可能无法画出图视图

上面的图可以看作
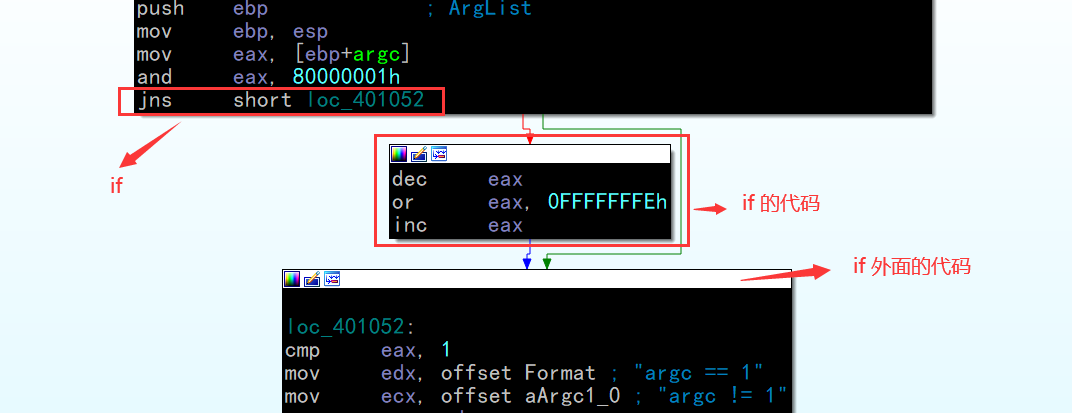
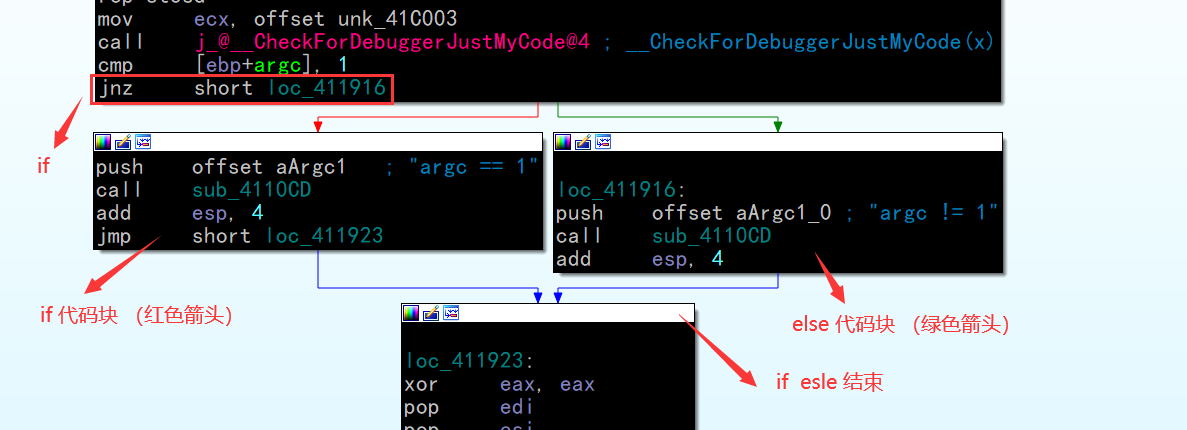
if elseif 为了方便看清结构,可以转化成 if else 的嵌套,因为 if elseif 的图视图 结构比较复杂不便于理解
缩略图
快速了解代码结构
IDA调试
下断点: 选中行 F2 或者 F5 再 F2下断点
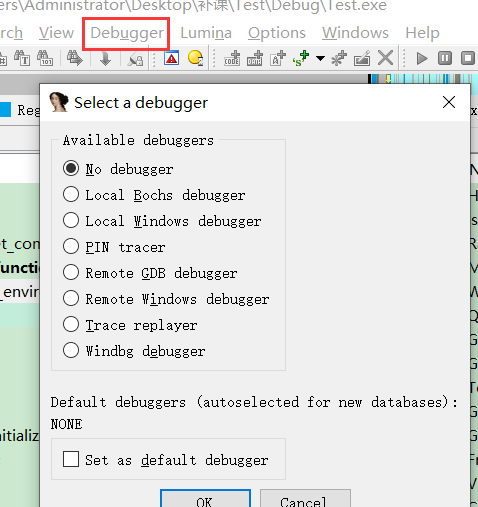
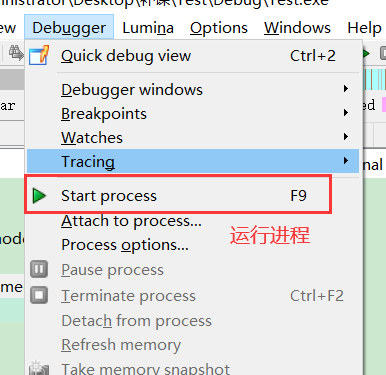
快捷键和 OD一样