X86C++反汇编03.除法的优化

大理寺少卿

1. 理解并掌握数学模型,这样换个编译器优化,数学模型是不变的
2. 同一模型,描述的代码序列可能会有变化

无符号数除法,且除数非2的整数次幂 的正数

令 M = 2^n / C

A / C => A 1 / C => A 2^n /C 1 / 2^n => A 2^n /C >> n => AM >> n

M = 2^n / C

C = 2^n / M

C是常量 n的值由编译器给那么还是常量

当M值越大,即 n值越大 数值越精确

因为我们是 32位除法,n值起步32 ,随着C的值越大,n的值越大

计算机会自动生成 满足条件的最小 M 值

因此可用定式 表达

mov eax, M ; MagicNumber

mul A ; AM

shr edx , n ; >>n

*int main(unsigned int argc, char argv[])**

{

printf("%d\r\n",****argc / 3** );**

return 0;

}

对应的反汇编代码

mov eax, 0AAAAAAABh ;M值 2863311531

*mul [esp+argc] ; A M**

shr edx, 1 ; n = 32+1 = 33 ,乘积 结果表达式为 edx(高32位) eax(低32位) ,右移32位

; 就到了edx, edx又右移了1位 就是 33,即 直接右移edx,默认已经右移了32位

push edx

push offset aD

call sub_401020

add esp, 8

xor eax, eax

retn

验证:

移位是下整,还原就需要上整

2^33 / 2863311531 = 8589934592/2863311531 = 3 即 C (被除数是3)

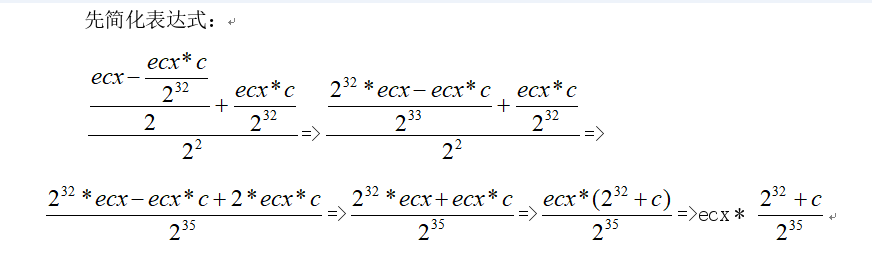
*int main(unsigned int argc, char argv[])**

{

printf("%d\r\n",****argc / 7** );**

return 0;

}

对应的反汇编代码

mov ecx, [esp+argc]

mov eax, 24924925h ;M有进位, 所以真正值为: 124924925h 4908534053

mul ecx

sub ecx, edx

shr ecx, 1 ;右移了 1 位

add ecx, edx

shr ecx, 2 ;右移了 2 位

*验证: 当遇到 - 移 + 移 代表 M 产生了进位 高位为1 右移32位 + 3位 总共移了 35 位**

2^35 / 4908534053 = 34359738368 / 4908534053 = 7

上面优化的原因就是图片倒过来转化,从终点推导到起点

是为了解决 M值是 大数问题 把 2^35 拆分成 2^32 2 2^2

练习: 还原代码

.text:00401001 mov esi, [esp+4+argc]** .text:00401005 mov eax, 0CCCCCCCDh 3435973837 .text:0040100A mul esi .text:0040100C shr edx, 2 2^34 17179869184 .text:0040100F push edx .text:00401010 push offset aD ; "%d\r\n" **.text:00401015 call printf

17179869184 / 3435973837 = 5

还原代码为 : argc/5

.text:0040101A mov eax, 20000003h 536870915** .text:0040101F mul esi .text:00401021 shr edx, 1Dh 2^61 .text:00401024 push edx .text:00401025 push offset aD ; "%d\r\n" .text:0040102A call printf .text:0040102F add esp, 10h**

argc / -23

2^61 / 536870915 = 4294967273(FFFF FFE9) = -0x17 = -23

无符号数 / 有符号数 结果是无符号数

*无符号数 有符号数 结果是有符号数**

有符号数除法,且除数非2的整数次幂 的正数

有符号就要面对 负数向上取值 ,正数向下取整问题

当 x 不为整数时 x 下整 +1 = x 上整

M = 2^n/C 因为 C 不是的整数次幂 ,因此 M 也不可能是,而且M是个小数

int main(unsigned int argc, char* argv[])
 {
    printf("%d\r\n",argc / 5);
    return 0;
 }
 对应的反汇编代码
 mov     ecx, [esp+argc]
 mov     eax, 66666667h    ; 1717986919
 imul     ecx                           ;  imul     代表有符号运算
 sar        edx, 1                     ; 2^33       8589934592
 ;下面代码是想实现无分支实现 下整转上整  还原代码时不需要还原
 mov     eax, edx
 shr        eax, 1Fh
 add      edx, eax

 下整转上整还可以用下面序列
 mov     eax,edx
 cdq
 sub     eax,edx

 验证:       8589934592  /   1717986919 = 5




 int main(unsigned int argc, char* argv[])
 {
    printf("%d\r\n",argc / 3);
    return 0;
 }
 对应的反汇编代码
 mov     ecx, [esp+argc]
 mov     eax, 55555556h       ;1431655766
 imul    ecx
 ;无分支实现 下整转上整 
 mov     eax, edx
 shr     eax, 1Fh
 add     edx, eax
 上面没有    sar        edx ,n    ,代表右移了  32位 
 所以:
 2^32  /  1431655766  =  3


 int main(int argc, char* argv[])
 {
    printf("%d\r\n",argc / 7 );
    return 0;
 }
 对应的反汇编代码
 mov           ecx, [esp+argc]
 mov           eax, 92492493h       ;2454267027
 imul           ecx                             ;这里把M变成了有符号负数
 add            edx, ecx                    ;调整结果
 sar              edx, 2
 ;无分支实现 下整转上整 
 mov           eax, edx
 shr             eax, 1Fh
 add            edx, eax

 结论:  当 M 值 为有符号负数时 ,需要对结果进行调整  有增加一条 调整指令
 调整方式为:      add       edx , 乘数指令操作数

 练习:
 .text:00401001           mov esi, [esp+4+argc]
 .text:00401005           mov eax, 38E38E39h            954437177
 .text:0040100A           mul esi                                     ;无符号数
 .text:0040100C           shr edx, 1                                 2^33        8589934592

 858934592  /   954437177  = 9             

 .text:00401019           mov eax, 86186187h            ; 186186187h     6544712071
 .text:0040101E           mul esi                                     ;无符号数
 .text:00401020           mov eax, esi
 .text:00401022           sub eax, edx                       
 .text:00401024           shr eax, 1
 .text:00401026           add eax, edx
 .text:00401028           shr eax, 4                                 2^(32+1+4)   = 2^37          137438953472            

 出现了  *  -  移  +  移指令   M产生了进位
   2 ^37   /    6544712071  =  21            


 .text:00401036           mov eax, 2AAAAAABh          715827883
 .text:0040103B           imul esi                    ;有符号
 .text:0040103D           sar edx, 1                 2^33            8589934592
 .text:0040103F           mov ecx, edx          ;无分之实现下整转上整
 .text:00401041           shr ecx, 1Fh                               
 .text:00401044           add edx, ecx

 2^33 / 715827883 =  8589934592 /  715827883  =  12

 .text:00401051           mov eax, 0EA0EA0EBh          3926827243
 .text:00401056           imul esi                                   ;有符号
 .text:00401058           add edx, esi                           ;M时有符号负数 调整指令
 .text:0040105A           sar edx, 5                                2^37      137438953472
 .text:0040105D           mov eax, edx                        ;无分之实现下整转上整
 .text:0040105F           shr eax, 1Fh
 .text:00401062           add edx, eax

 137438953472  /    3926827243  = 35

有符号除法定式

mov eax, M

imul r32/m32

sar edx , n

mov r32 , edx

shr r32, 31

add edx, r32

* 实现 用一个有符号数 A 无符号数 8086h ,要求结果为 有符号数 **

mov   ax, 8086h
 imul  A           
 add   dx,A        


 使用  imul 是因为 8086h是常量,而 A 是变量,使用muld的话结果不可控


 使用  imul  A  即 把 A * 8086h 的时候 实际运算的值的真值是(8086h 被视为有符号负数,最高位为1,他是取反+1后的值);

 add   dx,A    是因为要的结果是 8086hA ,但他运算的结果 为  8086hA  -  10000hA ,因此要加上                   10000hA

补码变形

a + ~a = ffff

a + ~a +1 = 10000h

~a+1 = 10000h - a

* A - ( 10000h - 8086h) **

*= A ( 8086h - 10000h )**

= 8086hA - 10000hA

在 dx,ax 中存一个只 32位的值

*ax10000h = ax.0000 = dx + ax ,ax**

xxxxbzn1

楼主，不论什么情况你一定要hold住！hold住就是胜利！