|
|
逆向一个序列号有3种层次
- 打个补丁,改一下跳转(暴力破解)
- 推导出一组可以用的账号密码
- 还原算法,并写出例算法(注册机,彻底破解)
彻底破解的难点是还原算法,和 写出例算法(可能变成解题问题)
优化
优化方向
- 体积优化
- 内存优化 例如:大数据 , 蓝光视频 ,写shellcode
- 磁盘优化 例如: 病毒 压缩
- 速度优化
现在的优化一般以执行速度为主,Debug版优化是以便于调试为主所以里面带有详细的信息,效率是次要的,但是并不代表不优化
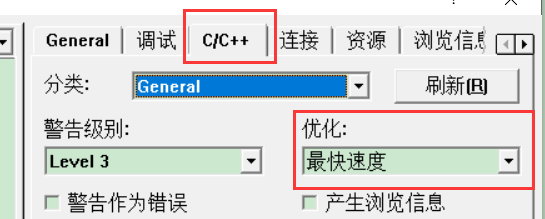
编译器对算法进行编译,运算结果的参与传递才会参与编译,否则不会参与编译(Debug 和Release 都会这样 )
参与传递的3种情况
- 传参
- 传返回值
- 赋值运算
例如下面代码:

运行会发现此处的断点是无效的,而且通过反汇编窗口看,是没有反汇编的代码的,因为他没有参与编译
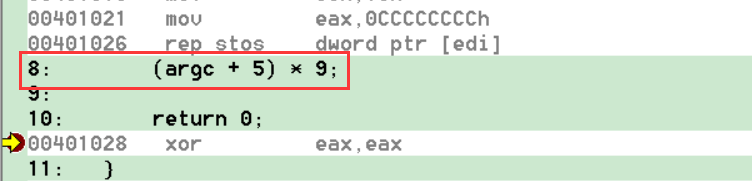
整形加法的优化

Release
把上述代码生成的 Release 版 文件用IED查看,会发现代码都被优化掉了
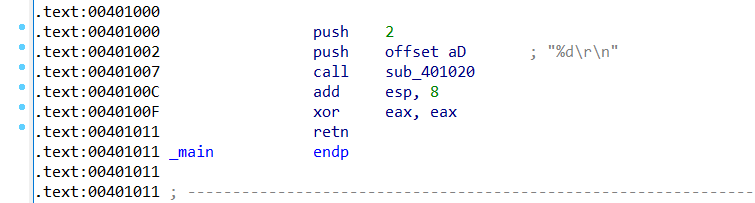
Debug
Debug也会优化,但不会优化得那么彻底,因为那样无法单步,只会在单行代码内优化,和把当行代码换成等价的更优代码,例如: -5 可能 +5的补码
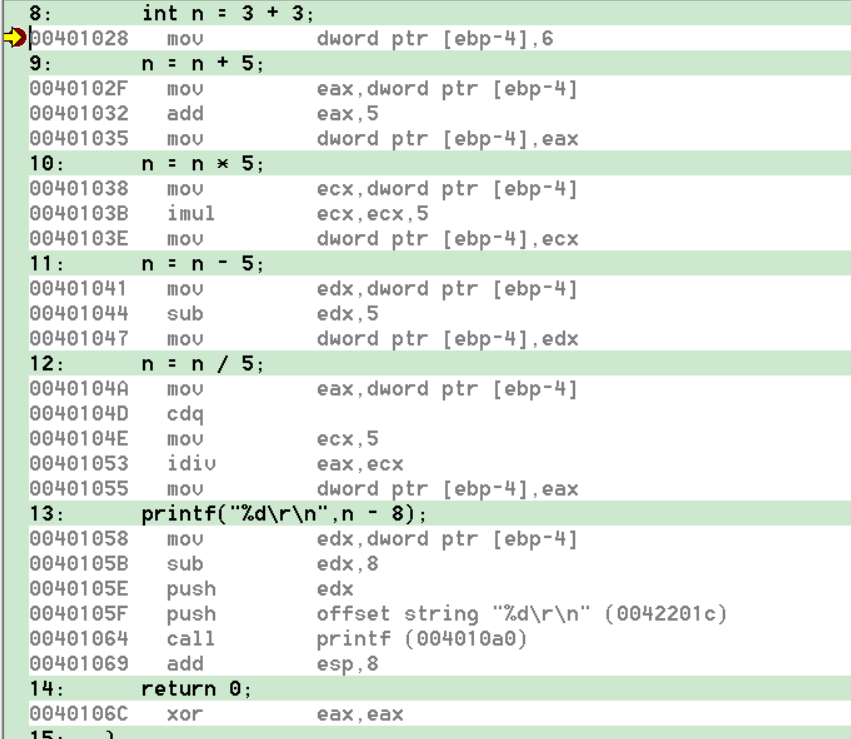
窥孔优化
窥孔优化: 优化一段代码,以几行为单位进行优化,如果源码发生了优化,
就会回到第一行开始重新开始,直到源码没有发生改变
- 常量传播: 假如一个变量初始化或者赋值为常量,值中间没有任何修改, 然后把他代入到另一个表达式的时候,可以用常量直接替换掉他
- 常量折叠:一个表达式,不管多复杂,只要参与运算的都是常量 ,就会触发常量折叠,编译期间直接对表达式求值,获得最后的常量结果
- 删除未使用的变量: 如果优化到最后,变量没有使用,就直接删除
1 int n = 3 + 3;
2 n = n + 5;
3 n = n * 5;
4 n = n - 5;
5 n = n / 5;
6 printf("%d\r\n",n - 8);
return 0;
1 触发常量折叠 3+3 直接变成6 int n= 6
2 触发常量传播 用6直接替换 n = 5+6 源码发生改变 从来开始
到 2 又 再触发常量折叠 n = 11 在从 1 开始
3 触发常量传播 用11 直接替换n n = 11 * 5; 源码发生改变 从来开始
到3又触发常量折叠 n = 55 ; 源码发生改变 从来开始
4 触发常量传播 用55直接替换n n = 55 - 5 源码发生改变 从来开始
到4又触发常量折叠 n = 50 ; 源码发生改变 从来开始
5 触发常量传播 用50直接替换n n = 50 /5 源码发生改变 从来开始
到5又触发常量折叠 n = 10 ; 源码发生改变 从来开始
6 触发常量传播 用10 直接替换n printf("%d\r\n",10 - 8); 源码发生改变 从来开始
到6又触发常量折叠 printf("%d\r\n",2); ; 源码发生改变 从来开始
到6又触发删除未使用的变量 printf("%d\r\n",2); 前面的代码直接删除
所以最后优化后编译的代码就是
printf("%d\r\n",2);
窥孔一方面用来优化代码,把代码由多变少,换个方向就是写反逆向工程 (代码混淆膨胀),把代码由少变多(只需要稳定可靠的的让1 行代码变2行就可以),2者互为对抗
VC6.0导出汇编代码
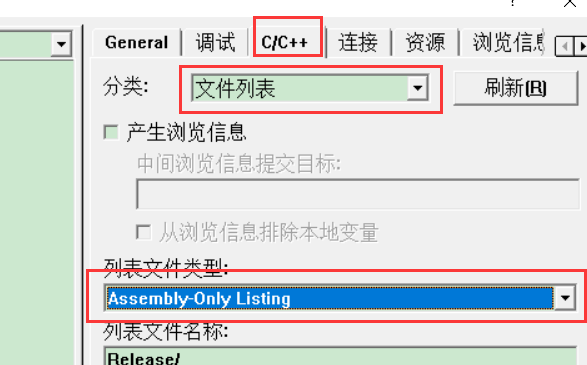
设置之后编译构建就会产生源码对应的汇编文件,再通过命令行编译和链接就可以产生 可执行文件,
只需要对对应的汇编文件进行混淆就可以了
乘法优化
- 常量 乘 常量 直接折叠
- 变量 乘 常量
Debug

注意 shl eax,3 等价于 lea eax ,[ eax * 8 ]
lea eax ,[ eax * n ] = mul eax , n n必须是2的整数次幂
Release
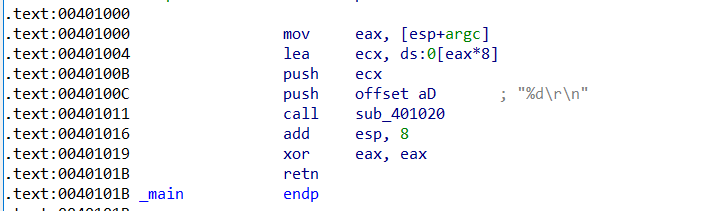
-
常量不是 2 的整数幂 拆分成 2的整数次幂的组合 ,但是高版本取消了这个的优化
-
例如:
argc 7 = argc 8 - argc
对应的汇编代码是
lea eax ,[ eax * 8 - eax ]
argc 25 = (argc 5)*5
对应的汇编代码是
mov eax,argc
lea eax ,[ eax 4 + eax ] 折叠就是 argc 5
lea eax ,[ eax 4 + eax ] 折叠就是 (argc 5) 5 => argc 25
argc 52 =( argc + (argc 3)4) 4
对应的汇编代码是
mov eax,argc
lea ecx,[ eax 2 + 1] 就是 argc 3
lea edx,[ eax + ecx 4 ] 就是 ( argc + (argc 3)*4) 折叠一下 就是 argc ** 13
shl edx,2 就是 *argc 13 4 折叠一下 就是 argc 52
- 变量 * 变量 无法优化
argc * argc
对应的汇编代码是
mov eax,argc
mov ecx,eax
imul ecx,eax
除法优化
高版本和低版本都会对除法进行优化,因为除法消耗比较大
- 当除数是变量,没有优化空间
- 无符号数除法,且除数时2的整数次幂
直接右移位
- 有符号数除法,且除数时2的整数次幂
计算机除法有取整问题
正数 或者 无符号数 除法 结果都是像下取整
负数 除法 结果都是像上取整
即 计算机的有符号 除法 是向0 取整的
所以在计算机中 (-a)/b != -( a/b)
在计算机中求以下结果
a / b = q 余 r
r = a - q*b
10 % 3 = 1 // r = 10 - 3 * 3 = 1
-10 % 3 = -1 // r = -10 - ( - 3 ) * 3 = -1
10 % - 3 = 1 // r = 10 - ( - 3 ) * (- 3) = 1
-10 % -3 = -1 // r = -10 - 3 * (- 3) = - 1
从上面可以看到 余数的符号 跟 被除数相关(即符号相同)
除法原型:
a / b = c .... r
6 / 4 = 1 ...2
- |r| < |b| : 余数的绝对值,绝对会小于除数的. 比如 6 / 4 = 1 .... 2 那么 余数2 不关是正数还是父数,绝对都是绝对会小于除数的,也就是4
2. a = c b + r : 求被除数,被除数是商除数+余数
3. b = (a - r)/c : 求除数,除数等于 被除数-余数 / 商
4. c = (a - r)/b : 求商: 被除数 - 余数 / 除数
5. r = a - (c b) : 求余数 被除数 - (商 除数)

从上面可以知道
A / 2^n
当 A > 0 , 结果需要 向 下取整
当 A < 0 , 结果需要 向 上取整 那么就等于 ( A + 2^n -1 ) / 2^n 向下取整
所以
argc / 4
当 argc > 0 = argc >> 2
当 argc < 0 = ( argc + 4 - 1) >> 2
所以
if( argc >= 0){
argc / 4 == argc >> 2
}
else
{
argc / 4 == ( argc + 4 - 1) >> 2
}
但是上面有分支,如何实现无分支呢
cdq 指令,如果eax 不小于0 那么edx 为0 ,否则为 -1
mov eax , argc
cdq ; eax >= 0 , edx =0 否则 eax<0 ,edx = 0xFFFFFFFF
and edx ,3 ; eax >= 0 , edx =0 , edx = 0 否则 eax<0 ,edx = 0xFFFFFFFF dex=3
add eax,dex ; eax >= 0 , edx =0, edx = 0 ,eax=0 否则 eax<0,edx = 0xFFFFFFFF,dex=3, eax=3
shr eax,2 ;eax >> 2
因此可以得到代码定式
a / 2^n 的反汇编代码是
1 mov eax , a
2 cdq
3 and edx ,2^n - 1
4 add eax,dex
5 shr eax, n
必须要验证一下 第3行 是否满足 值 等于 第5行的 2^n -1 例如
1 mov eax , a
2 cdq
3 and edx , 7
4 add eax,dex
5 shr eax, 2
是错的 7 != 2^2 -1
argc / 2
1 mov eax , a
2 cdq
3 sub eax,dex ; 2^n -1 ,n = 1 => 1 = 0 - (-1)
4 shr eax, 1
注意除数是2情况有些特殊 ,指令序列不一样但数学模型是一样的
练习:
argc / 32
1 mov eax , a
2 cdq
3 and edx ,31
4 add eax,dex
5 shr eax, 5
VC6 .0 字体补丁
正常情况下VC6.0 可选字体很少,因此需要打补丁
用OD 附加 进程 VC6.0
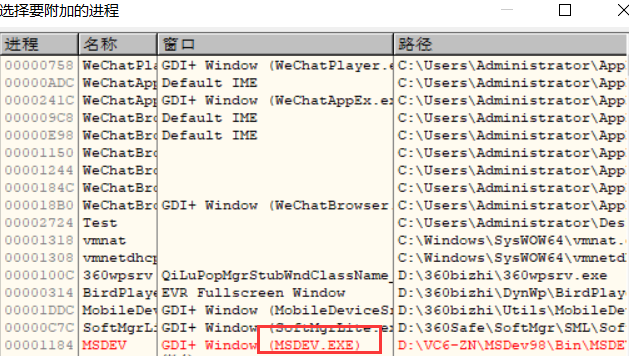
当我们选择字体时,肯定要用到列举字体的函数
列举字体的函数的函数为 EnumFontFamiliesEx 在 Gdi32.lib 里面
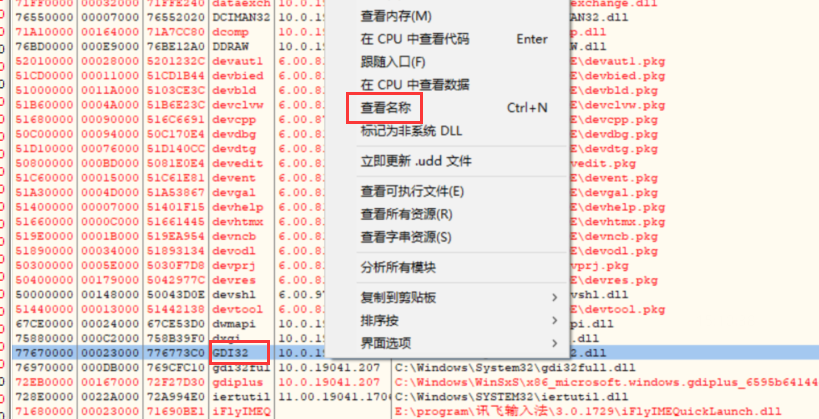
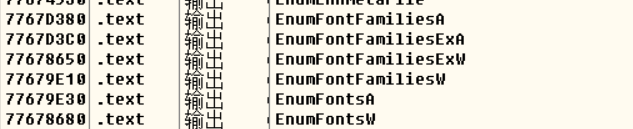
函数比较多,无法确定使用哪一个,可以到主模块去看看

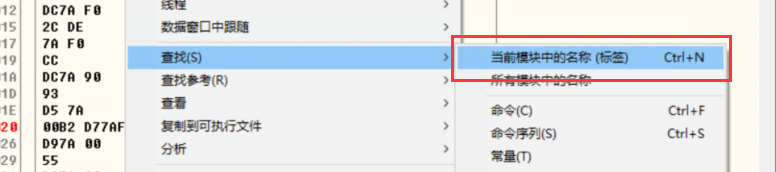
可以看到是这个

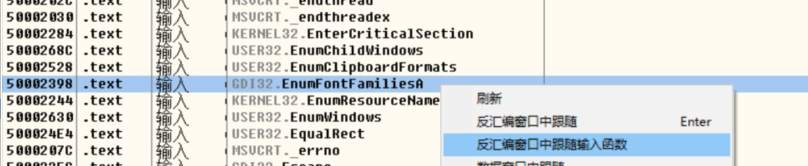
下断点,因为我们换字体肯定会调这个函数
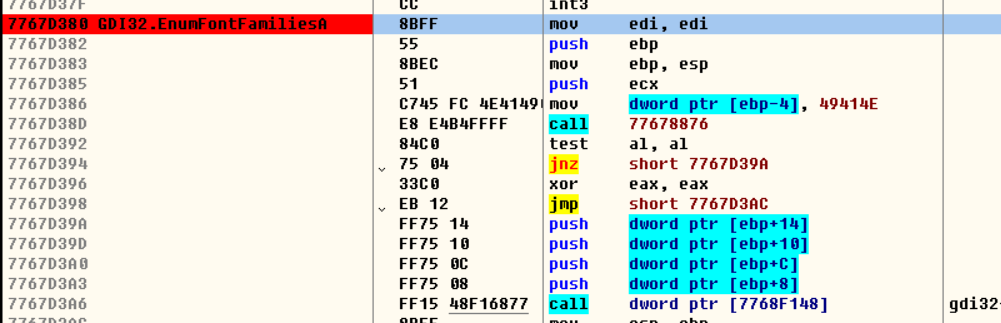
去换字体就会断下来,继续跟可以发现有检查,那如果把检查跳转去掉不跳走直接 执行下面的指令
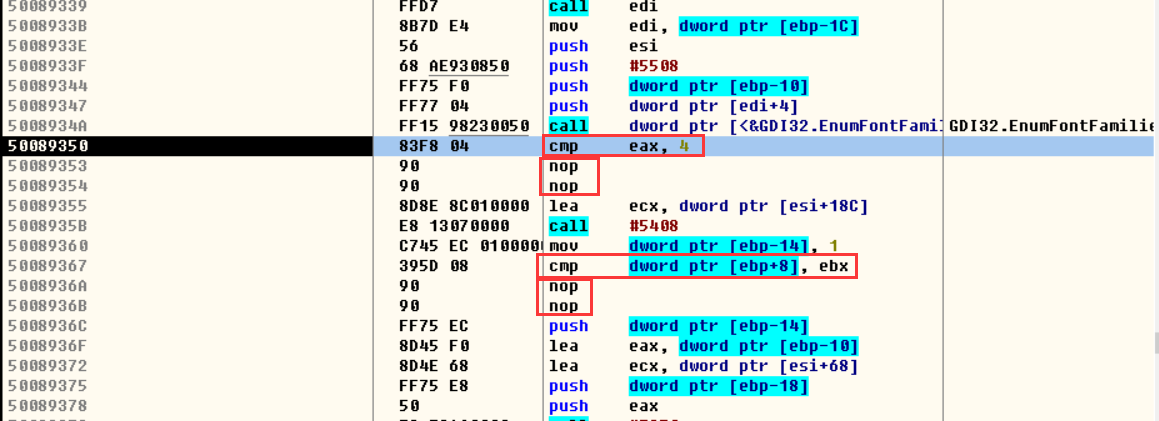
然后把修改复制到可执行文件,覆盖掉原来的 dll 就可以了,再去看就可以发现字体多了
|
|